ADVANCED PROPULSION SYSTEMS (APSYS) LAB
High Speed Propulsion Lab in IIT Kharagpur, India
ABOUT
The APSYS lab is located at 001 ground floor of Annex Building in the Aerospace Engineering Department, IIT Kharagpur, India. Research on high speed propulsion, pulse jet ignition, vortex combustion, thermoacoustics, spark ignition, jet deflection, etc is being conducted experimentally and computationally. The group performs flow imaging, flow diagnostics, pressure measurements on scaled down test objects. Members have access to a super-computing facility for running computer codes like Fluent, SU2, OpenFoam etc. The Lab has a dedicated compressed air facility, a direct connect modular flow facility capable of running various aerothermodynamic studies. A team of PhD students, MTech students and Undergrad students work on various projects.
NEWS AND ANNOUNCEMENTS
APSYS Labs receives DST funding for turbulent combustion research. The funding will cover equipment procurement for pressure measurements and the purchase of specialty gases used in the tests.
General Information
Areas of research include combustion oscillations, vortex driven flows, pulsating flows, method of characteristics, combustion sciences etc.As part of our work in high speed combustors, we are studying flame behavior, ignition, stabilization, flashback and mode transition in high speed combustors both with cavity assisted and strut assisted flame stabilization mechanisms. As part of our work on Combustion Instability prediction and control, we are also looking at vortex driven resonant combustion in Gas Turbine combustors. Active combustion control using secondary injection targeting q' oscillation tailoring are being attempted.
PEOPLE
Instructors, Students, Collaborators, RAs, TAs etc.
Current Members
Past Members
POSTS FROM THIS GROUP
Posts about publications, achievement, facilites, books from this group
Gaps in Understanding Combustion Dynamics of Scramjet Engines
Amardip Ghosh #Advanced Propulsion Systems (APSYS) Lab
https://doi.org/10.1016/j.ast.2025.111046 Scramjet combustion dynamics remain among the most complex and least understood areas in high-speed airbreathing...
Read more
TBCC RBCC Mode switch challenges
Amardip Ghosh #Advanced Propulsion Systems (APSYS) Lab
TBCC vs RBCC Transition Challenges TBCC (Turbine-Based Combined Cycle) — Compressor-Side Issues 1. Primary operability risk: compressor surge, stall, blade choking as inlet total temperature and pressure ratio rise; downstream back-pressure transients...
Read more
A Matlab code of how to do dynamic mode decomposition of a video sequence.
Amardip Ghosh #Advanced Propulsion Systems (APSYS) Lab
A Matlab code of how to do dynamic mode decomposition of a video sequence. (ChatGPT) % DMD on a Video Sequenceclear; close all; clc; %% Load VideovideoFile = 'video.mp4'; % Change to your video filev = VideoReader(videoFile); % ParametersresizeFactor = 0.25; % Reduce size to speed upnumFrames = min(100, floor(v.Duration * v.FrameRate)); % Limit number of frames % Read and preprocess video framesX = [];...
Read more
Bychkov Limit (ChatGPT, Google AI)
Amardip Ghosh #Advanced Propulsion Systems (APSYS) Lab
The Bychkov limit, also known as the detonation cell size limit, is a concept in detonation physics that describes the minimum size of a detonation...
Read more
Independent Component Analysis (ICA) for a video sequence. ChatGPT
Amardip Ghosh #Advanced Propulsion Systems (APSYS) Lab
%Here's a MATLAB code that performs Independent Component Analysis (ICA) on a video sequence. The goal is to treat each frame as a data %vector and then extract statistically independent components from this set using ICA. %This is particularly useful for motion segmentation...
Read more
Principle Component Analysis (PCA) Matlab Code (ChatGPT)
Amardip Ghosh #Advanced Propulsion Systems (APSYS) Lab
% PCA on an image setclc; clear; close all; % Set image directoryimageDir = 'images/'; % Change this to your image folder pathimageFiles = dir(fullfile(imageDir, '*.png')); % Change extension if needed (e.g., .jpg, .bmp)numImages = length(imageFiles); % Read first image to get dimensionsfirstImage = imread(fullfile(imageDir, imageFiles(1).name));if size(firstImage, 3) == 3firstImage = rgb...
Read more
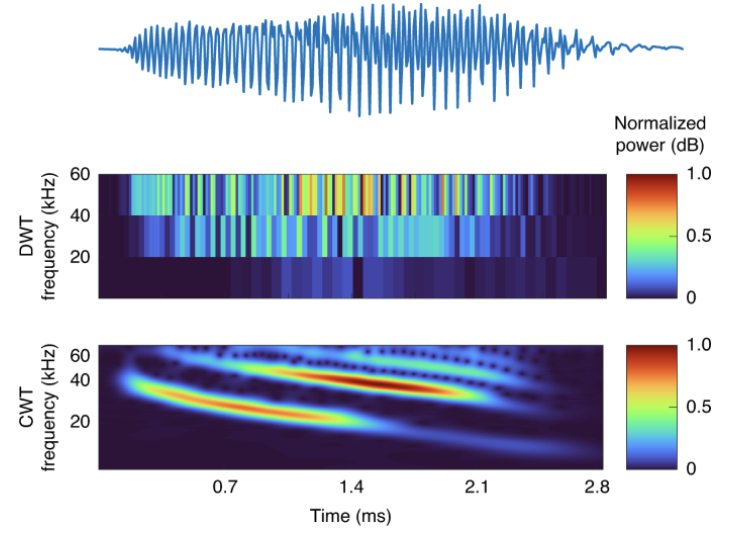
Wavelets in Signal Processing
Amardip Ghosh #Advanced Propulsion Systems (APSYS) Lab
Above Image is from Arts, L.P.A., van den Broek, E.L. The fast continuous wavelet transformation (fCWT) for real-time, high-quality, noise-resistant time–frequency analysis. Nat Comput Sci 2, 47–58 (2022). https://doi.org/10.1038/s43588-021-00183-z How does wavelet transform differ from spectrogram when used on the same time series data ? ChatGPT : Both wavelet transform and spectrograms are time-frequency analysis tools, but the...
Read more
Insights into flame flashback phenomenon utilizing a Strut-Cavity flame holder inside scramjet combustor
Pranay Singeetham #Advanced Propulsion Systems (APSYS) Lab @Amardip Ghosh
Understanding upstream flame propagation in scramjets is challenging, particularly concerning flame flashback in a combustor with a novel strut-cavity flame holder. Two-dimensional unsteady Reynolds-averaged Navier–Stokes (URANS) simulations were performed to investigate how Mach number and wall divergence affect flame behavior. The utility of the strut-cavity flame holder was highlighted through a study of its non-reacting flow characteristics. Flow dynamics are significantly altered as the...
Read more
SCRAMJET Test Rig Instrumentation
Amardip Ghosh #Advanced Propulsion Systems (APSYS) Lab
The rig is being instrumentated for transitioning from cold flow supersonic mixing studies to reacting flow mode transition studies.
...Read more
Attachments
| 1. Minwook Chan PhD Thesis | |
| 2. PhD Thesis |
Thermodynamics and Aerospace Propulsion Systems Class
Amardip Ghosh #Advanced Propulsion Systems (APSYS) Lab
Aerodynamics, Thermodynamics, Heat Transfer and Combustion Chemistry. The building blocks of propusion systems. While feedback control is also an integral part, courses like these primarily cover the mechanical aspects of propulsion systems.
...Read more
"Thank you for shaping the future with your wisdom, dedication, and guidance. Your impact on our life is immeasurable, and we are forever grateful. Happy Teacher’s Day!"
...
Flame oscillations under certain flow and equivalence ratio conditions can be controlled using open loop and closed loop controls. Different flame shapes, lift off characteristics can be observed, along with periodic behavious in flame anchoring location. Flame heat release modulations, anchoring, oscillations suppression using acoustic forcing and the effect of resonant burning on NOx emission are important topics of research being addressed.
...
BROWSE POSTS
Find content on publications, achievement, facilites etc
RECENT POSTS
Posts arranged recent first
CONTACT Advanced Propulsion Systems (APSYS) Lab
Emails through this form are monitored for spam
7846 1 1 1
FEATURED POST
BTP and MTP Project Topics - 2023 Batch
Amardip Ghosh #Advanced Propulsion Systems (APSYS) Lab
This year we have a large number of BTP and MTP students as well as students from outside schools interning with our lab. While we remain open to project suggestions from students and sponsors, we also want to create a thematic focus of projects we want students to work on. If you have signed up with our lab for your BTP, MTP or Summer Internship, you can go over the list of topics we are proposing. Also read up the literature in the attachments section. You may be able to extend the work des...
Read more
Attachments